Inequalities Class 9

Exercise :

1. In △ABC, if AB < BC < AC, name the largest and smallest angles of the triangle.

In △ABC, AB < BC < AC

Solution. We know that the largest side has largest angle opposite to it.

In △ABC, AB < BC < AC

Here AC is the largest side and AB is the smallest.

∠B is the largest angle and ∠C is the smallest.

2. In △PQR, ∠P = 80° and ∠Q = 43°. Arrange the sides in descending order of length.

Solution :

We know that sum of three angles of a triangle is 180°.

In △PQR,

∠P = 80° and ∠Q = 43°

∠R = 180° - (80° + 43°)

= 180° - 123° = 57°

side opposite to largest angle ∠P is greatest and side opposite to smallest angle ∠Q is smallest.

Arranging the sides of △PQR in descending order, we have

QR > PQ > PR.

3. In △ABC, BC is produced to D so that AB = AC = CD. If ∠BAC = 72° , find the angles of

△ABD and arrange its sides in ascending order of length.

Solution .

In △ABC,

BC is produced to D so that AB = AC = CD.

∠BAC = 72°

(i) Find the angles of △ABD.

(ii) Arranged the sides of △ABD at ascending order of lengths.

In △ABC,

∠BAC = 72°

∠B + ∠C = 180° - 72° = 180°

But in △ABC,

AB = AC

∠B = ∠C = 180°/2 = 54°

∠B = 54°

in △ACD,

AC = CD

and exterior ∠ACB = ∠CAD + ∠D

54°= ∠D + ∠D

54° = 2∠D

∠D = 54° / 2 = 27°

and ∠BAD = 72° + 27° = 99°

Now in △BAD, we have

∠A = 99°,

∠B = 54°

∠B = 27°

We know that side opposite to the greatest angle is greatest.

BD > AD > AB

or AB < AD < BD.

Q 4. In △MPN, MP = 11 cm, PN = 5cm and MN = 7cm. Arrange the angles of △MPN is ascending order.

Solution :

In a triangle, greater sides has greater angle opposite to it since MP > MN > PN

∠N > ∠P > ∠M

or ∠M < ∠P < ∠N.

Q 5. Is it possible to draw a triangle whose sides are of following lengths ? Give reason.

i) 6.5 cm, 3.2 cm, 9.7 cm

ii) 4.2 cm, 6 cm, 1.7 cm

iii) 3.9 cm, 5.2 cm, 3 cm

Solution.

In a triangle, sum of any two sides is greater than the third side.

i) Given sides are of lengths 6.5 cm, 3.2 cm, 9.7 cm

Here, 6.5 + 3.2 = 9.7

so, it is not possible to draw a triangle.

ii) Here , sum of two side of triangle

= 4.2 + 1.7 = 5.9 > 6

so, it is not possible to draw a triangle.

iii) Here , sum of two side of triangle

= 3.9 + 3.0 = 6.9 > 5.2

so, it is possible to draw a triangle.

Q 6) Arrange the sides of △ABC in ascending order of their lengths.

Solution :

In △ABC

∠EAB = 95° and = ∠ACD = 125°

Now,

In △ABC

∠EAB + ∠BAC = 180°

95° + ∠BAC = 180°

∠ BAC = 180° - 95°

∠ BAC = 85

similarly,

∠ACD + ∠ACB = 180°

125° + ∠ACB = 180°

∠ ACB = 180° - 125°

∠ BAC = 55°

But

∠A + ∠B + ∠C = 180°

85° + ∠B + 55° = 180°

∠B + 140° = 180°

∠B = 180° - 140° = 40°

Now, ∠A = 80° , ∠B = 40° , ∠C = 55°

Greater angle has greater side opposite to it.

Since , ∠A > ∠C > ∠B

BC > AB > AC

Q 7) In the given figure, AB is perpendicular to AD and BC. Also ∠C = 40 , ∠D = 30 . Which is longer AO or BO ?

Solution:

In the given figure,

AB ⊥ AD and AB ⊥ BC

∠C = 40°, ∠D = 30°

In △ADB, ∠A = 90°, ∠D = 30°

∠ABD or ∠ABO = 180° - ( 90° + 30°)

= 180° - 120°

= 60°

Similarly in △ACB; we have

∠BAC = 180° - ( ∠ABC + ∠C)

= 180° - (90° + 40°)

= 180° - 130°

= 50°

Now ,in △AOB, ∠BAC or ∠BAO = 50°

and ∠ABD or ∠ABO = 60°

∠AOB = 180° - (50° + 60° ) = 180° - 110° = 70°

∠ABO > ∠BAO

AO > BO

Q 8) In △PQR, PQ = PR. QR is extended to a point S. Prove that PS > PQ.

Solution :

In △PQR, we have

PQ = PR

∠Q = ∠R

In △PRS, we have

Ext. ∠PRQ = ∠RPS + ∠PSR

or ∠PRQ ∠S

In △PQS, we have

∠Q = ∠S ( ∠Q = ∠R or ∠PRQ )

PS > PQ ( Greater angle has greater side opposite to it.)

Hence proved.

Q 9) In △ABC, P is any point inside it. Prove that ∠BPC > ∠A.

Solution :

Produce BP to meet AC at Q

Ext. ∠BPC > ∠PQC --------(i)

and

Ext. ∠BQC > ∠A ---------(ii)

From (i) and (ii), we have

∠BPC > ∠A

Hence proved.

Q 10) Prove that the perimeter of the triangle is greater than the sum of its three median.

Solution :

Given : In △ABC ,

AD, BE, and CF are its medians.

To prove : ( AB + BC + CA ) > ( AD + BE + CF)

Proof :

Sum of any two sides of triangle is greater than twice the median bisecting the third side.

so,

AB + AC > 2AD ----------------(i)

AC + BC > 2CF -----------------(ii)

BC + AB > 2BE ----------------(iii)

(i) + (ii) + (iii)

AB + AC + AC + BC + BC + AB = 2AD + 2CF + 2BE

2 ( AB + BC + CA) > 2 (AD + BE + CF)

AB + BC + CA > AD + BE + CF

Hence perimeter of a triangle is greater than the sum of its three medians.

Q 11) In △ABC, AB < AC, PB and PC are the bisectors of ∠B and ∠C. Prove that PB < PC.

Solution .

Given : In △ABC, AB < AC.

PB and PC are the bisectors of ∠B and ∠C.

To prove : PB < PC

Proof : In △ABC, AB < AC.

∠ACB < ∠ABC ( Angle opposite to smaller side is less than the angle opposite to greater side)

1/2∠ACB < 1/2∠ABC

∠PCB < ∠PBC

PB < PC

Hence Proved.

Q 12) In a quadrilateral ABCD, P is an internal point.

Proved that AP + BP + CP + DP > Semi-perimeter of quadrilateral ABCD.

Solution :

Given : P is any point inside the quadrilateral ABCD. PA, PB, AC and PD are joined.

To prove : PA + PB + PC + PD > 1/2 ( AB + BC + CD + DA )

Proof : In △PAB

PA + PB > AB ----------(i) ( sum of two sides of a triangle is greater than its third side)

similarly in △PBC, we have

PB + PC > BC ------------(ii)

and in △PCD. we have

PC + PD > CD -------------(iii)

and in △PDA, we have

PD + PA > DA ------------(iv)

Adding (i), (ii), (iii) and (iv)

PA + PB + PB + PC + PC + PD + PD + PA > AB + BC + CD + DA

2(PA + PB + PC + PD ) > AB + BC + CD + DA

AP + BP + CP + DP > 1/2(AB + BC + CD + DA)

Q 13 ) The side BA and BC of △ABC are produced to D and E respectively, Proved that

∠DAC + ∠ECA > 180°.

Solution :

Given : Sides BC and BA are produced to D and E respectively, Forming exterior ∠CBD and ∠ACE.

To prove : ∠DAC + ∠ECA > 180°

Proof : In a triangles

Exterior angle is equal to the sum of its interior opposite angles.

∠CAD = ∠B + ∠C ------------------(i)

and ∠ACE = ∠A + ∠B ------------------(ii)

adding (i) and (ii)

∠CAD + ∠ACE = ∠B + ∠C + ∠A + ∠B

∠CAD + ∠ACE = ∠B + 180° --------------------( ∠A + ∠B + ∠C = 180°)

∠DAC + ∠ECA > 180°

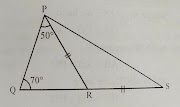
Q 14 ) In △PQR, ∠Q = 70°, ∠QPR = 50° and PR = RS. Proved that PQ < PS.

Solution.

Given : In △PQR, ∠Q = 70°, ∠QPR = 50° and PR = RS

To prove : PQ < PS

Proof :

In △PQR, ∠Q = 70°, ∠P = 50°

∠PRQ = 180° - ( 50 + 70)°

= 180° -120°

= 60°

But in △PRS, we have

Ext ∠PRQ = ∠PRS + ∠RSP

60° = ∠PRS + ∠RSP

RP = RS (given)

∠PRS = ∠RSP = 60°/2 = 30°

Now in △PQS, we have

∠S < ∠Q

PQ < PS (smaller angle has smaller side opposite to it )

Q 15) AD bisects ∠BAC of △ABC. Prove that AB > BD.

Solution :

Given : In △ABC, AD is the bisector of ∠A.

To prove : AB > BD.

Proof : AD is the bisector of ∠A

∠BAD = ∠CAD

Now in △ACD, we have

Ext. ∠ADB = ∠CAD + ∠C

∠ADB > ∠CAD

∠ADB > ∠BAD ( ∠CAD = ∠BAD)

AB > BD

Inequalities Class 9